Descifrando la Regresión: Una Mirada a su Significado y Pilares Fundamentales
En el mundo del análisis de datos, la regresión emerge como una herramienta indispensable para comprender las relaciones entre variables y realizar predicciones. Pero, ¿qué significa realmente la regresión y cuáles son los cimientos sobre los que se construye? En esta publicación de blog, exploraremos el significado de la regresión, desentrañaremos sus supuestos básicos y descubriremos cómo esta técnica puede iluminar el camino hacia el conocimiento.
El Significado de la Regresión: Más Allá de la Predicción
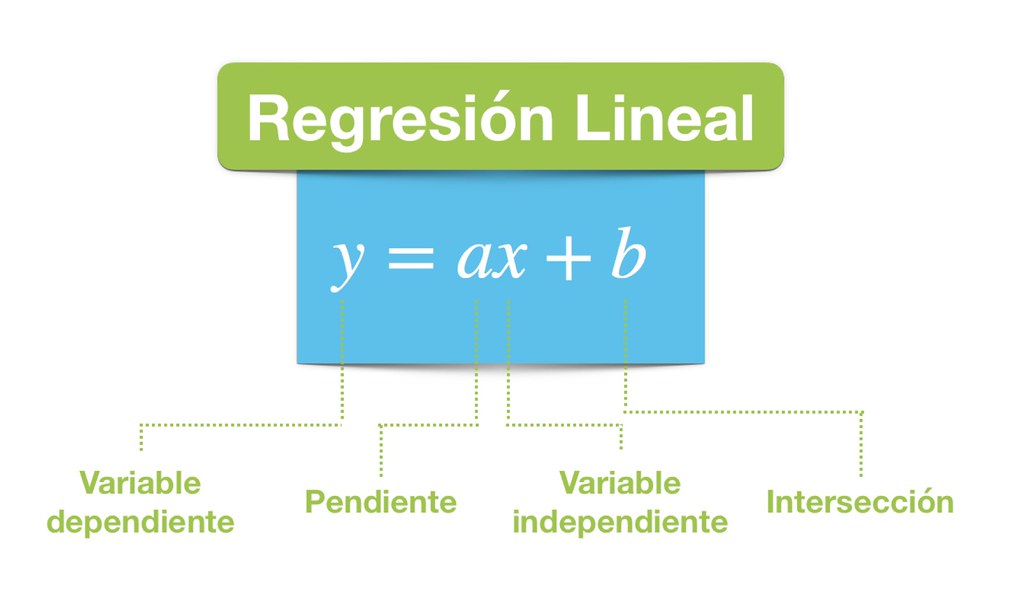
La regresión, en su esencia, es un modelo matemático que busca describir la relación entre una variable dependiente (aquella que queremos predecir o explicar) y una o más variables independientes (aquellas que creemos que influyen en la variable dependiente). Esta relación se materializa en una ecuación, como la fundamental de la regresión lineal simple:
Ŷ = a + bX
En esta ecuación:
- Ŷ representa el valor predicho de la variable dependiente.
- a es el intercepto, el valor de Ŷ cuando X es cero.
- b es la pendiente, que indica cuánto cambia Ŷ por cada unidad de cambio en X.
- X es el valor de la variable independiente.
A través de esta ecuación y los valores estimados de 'a' y 'b', la regresión nos permite no solo hacer predicciones precisas, sino también comprender cómo los cambios en las variables independientes (X) afectan a la variable dependiente (Ŷ). Por ejemplo, si 'b' es positivo, sabemos que un aumento en X se asocia con un aumento en Ŷ, y la magnitud de 'b' nos indica la fuerza de esta relación.
Los Pilares de la Regresión: Supuestos Básicos
Para que un modelo de regresión sea válido y confiable, debe cumplir con ciertos supuestos básicos. Estos supuestos son como los pilares que sostienen la estructura de la regresión y garantizan que los resultados obtenidos sean significativos y precisos.
- Linealidad: La relación entre las variables independientes y la variable dependiente debe ser lineal. Esto significa que un cambio en una variable independiente debe producir un cambio proporcional en la variable dependiente.
- Independencia: Las observaciones deben ser independientes entre sí. Esto implica que el valor de una observación no debe estar influenciado por el valor de otra observación.
- Homocedasticidad: La varianza de los errores debe ser constante para todos los valores de las variables independientes. En otras palabras, la dispersión de los puntos alrededor de la línea de regresión debe ser similar a lo largo de toda la línea.
- Normalidad: Los errores deben seguir una distribución normal. Esto significa que la mayoría de los errores deben estar cerca de cero, y los errores grandes deben ser menos frecuentes.
La Regresión en Acción: Aplicaciones y Ejemplos
La regresión encuentra aplicaciones en una amplia gama de campos, desde la economía y las finanzas hasta la medicina y la ingeniería. Por ejemplo, en economía, la regresión se utiliza para analizar la relación entre el gasto en publicidad y las ventas de un producto. En medicina, la regresión puede ayudar a predecir la probabilidad de desarrollar una enfermedad en función de factores de riesgo como la edad, el peso y el historial familiar.
Conclusión
Recursos Adicionales
Videos:
- [Video 1: Introducción a la Regresión Lineal]
- [Video 2: Supuestos de la Regresión Lineal]
- [Video 3: Aplicaciones de la Regresión Lineal]
- [Video 1: Regresión Lineal en Excel]
- [Video 2: Análisis de Regresión en Excel]
Blogs relacionados:
- Blog 1: [Regresión]
- Blog 2: [Introducción a la regresión lineal: definición y aplicaciones]






0 Comentarios